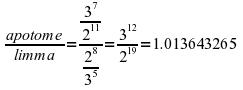
Ludger
Hofmann-Engl (for Musopen)
Croydon Family Groups
Part 1 - December 2009
Popular belief holds that there is a strong connection between musical and mathematical thinking. Whether this is true or not, there have been only a limited number of individuals who have applied computational means to music. However, particularly since the 2nd half of the 20th century some schools have emerged applying mathematical methods directly or indirectly to music.
1. Individuals making the connection between music and mathematics
This section does not claim to be comprehensive, but highlights simply important developments.
1. 1. Pythagoras (ca 570 – 495 BC)
No primary source exists on Pythagoras. However, Nicomachus (ca 120 – 60 BC) claims that it was Pythagoras who discovered that consonant and dissonant sounds are the result of number relationships with the diapason (1/2), diapente (2/3)and diatessaron (3/4) to be consonant but not so the tone in between the diapente and the diatessaron (8/9).
Additionally, the Pythagorean scale has been attributed to Pythagoras by placing consecutively fifths upon each other. This is: Fa – Do – So – Re – La – Mi – Si resulting in the scale: Do, Re, Mi, Fa, So, La, Si, Do. However, placing 7 octaves upon each other and 12 fifths, produces the Pythagorean Comma. This is:
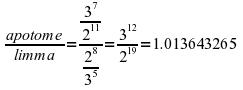
This comma amongst other commas has led to the introduction of the equal temperament in later times.
1.2. Euclid (around 300 BC)
Euclid wrote Κατατομη ανόνος (about the divisions on a the monochord). His work on the elements of music has been lost. The sectio canonis (below after Hawkins) contained in the Introductio Harmonica has been attributed to Kleoneides with high probability. The sectio canonis contains the instruction – to our knowledge for the first time in history - on how to divide the length of the monochord in order to obtain musical intervals.
Diapason = Octave
Diapente = Fifth
Diatessaron = Fourth
Diezeuctic tone = major Second
Limma ~ minor Second
While diapason, diapente and diatessaron belong, according to theorem XIX, to the unmovable sounds, the diezeuctic tone and the lima belong, according to theorem XX, to the class of moveable sounds.
1.3. Jing Fang (Chinese: 京房 78 – 37 BC)
According to a chapter within Hou Han Shu of Sima Biao (司馬彪 243 - 306 AD), it appears that Jing Fang was the first person to compute the
Mercator Comma. This is, overlaying 53 fifths and 31 octaves produces the near value of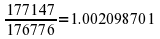 
which in cent
is:
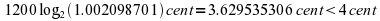(producing
a beat of about 1 period per 1 to 2 seconds).
1.4. Ptolomy (Greek: Κλαύδιος Πτολεμαῖος Latin: Klaúdius Ptolemaîus ca 90 – ca 168 AD)
Ptolomy wrote a three volumes comprising work called Αρμονικά (theory of music). He divides scales into tetrachords (interval of a fourth) and classifies those tetrachords according to their three internal intervals into 8 classes. The three main classes are:
Enharmonic
Chromatic
Diatonic
Chromatic itself is further subdivided into Soft and Intense, and Diatonic into Soft, Tonic, Diatonic, Intense and Equable. The Diatonic Intense Tetrachord is:
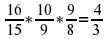
This is, a minor second (15/16) is followed by a small major second (10/9) and a large major second (9/8) which results in a fourth (4/3). This tetrachord corresponds to just tuning.
What is remarkable about Ptolemy's contribution is not only that he was
able to depict intervals in form of fractions
but that he understood that adding intervals, requires the fractions to be multiplied. This is:
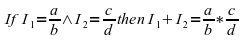
1.5. Francisco de Salinas (1513 – 1590)
In his History of the Science and Practice of Music (1776), John Hawkins reports that Salinas describes in the fifths chapter of his third book three different tuning systems. According to Hawkins, these are:
The Diatonic Genus as: 
The Chromatic Genus as: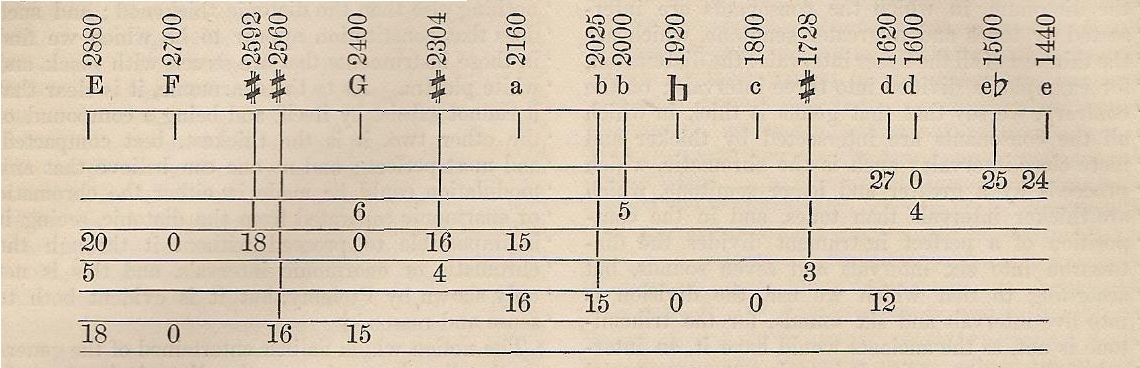 
The Enharmonic Genus as: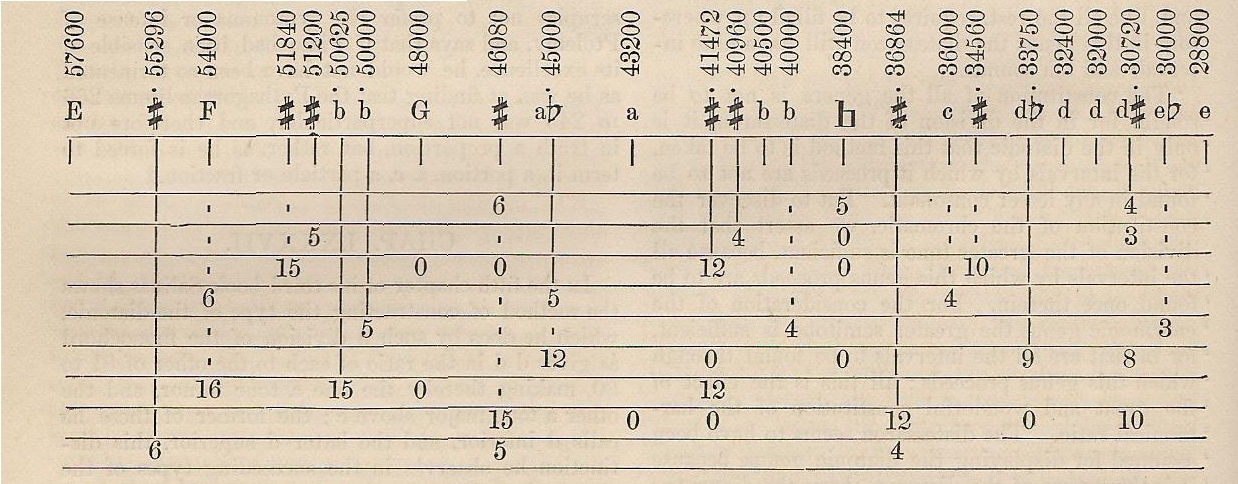 
1.6. Johannes Kepler (December 27, 1571 – November 15, 1630)
Kepler wrote the Harmonices Mundi
(The harmonies of the world) published by Gottfried Tamachius Tambach in 1619.
Here, Kepler expresses his fascination with the fact that the
ratio between maximum and minimum angular speed of the planets in
orbit corresponds to musical intervals. For instance, he observes
that the maximum and minimum angular speed of earth around the sun
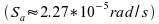corresponds to the interval
which in musical terms can be related to the interval of a minor second
(i.e. mi to fa). Taking into account the introduction of the cent calculation, equal temperament
and the discovery of categorical perception, we might conclude that Kepler's Harmonices Mundi appears
to be of historical value only. Still, what is truly surprising is
that Kepler's ideas are absurd from a physical point of view. It is
true that:
but still:
.
It is like saying: “Yesterday I ran 5 kg."
1.7. René Descartes (31 March 1596 – 11 February 1650)
In 1618, the 22 years old Descartes concludes his Musicae Compendium with the words:
Nec scirent hic, inter ignoraniam militarem ab homine desidioso et [non] libero, penitusque diversa cogitnati et agenti, tumultuse tui solius gratia esse compostium.
They don't know here, that amongst ignorant warmongers of lazy and constrained people who think and act completely different [to me], in restlessness this work was written for you.
Descartes shows in this compendium his clear understanding of modern and traditional music theoretical ideas, but he delivers apparently for the first time in history a stringent classification of consonances and dissonances as shown in the figure below taken from his compendium.
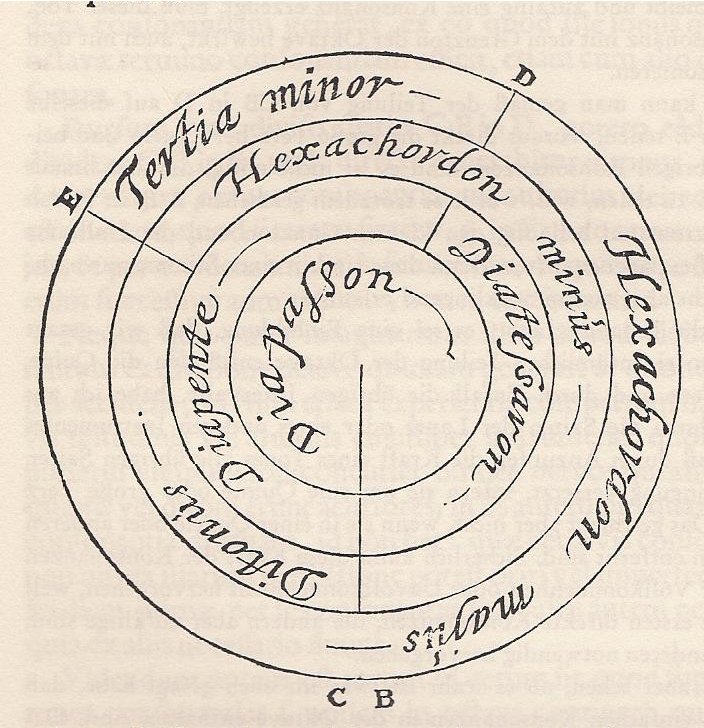
Here, Descartes puts the diapasson (octave) in the centre (most consonant), the diapente (fifths) and diatessaron (fourth) both into the next layer (less consonant), the hexachordon minus (minor sixth) and the diatonis (major third) into the next layer (even less consonant) and in the outside layer he places the tertia minor (minor third) and hexachordon majus (major sixth). Tritone and seconds are considered to be dissonant. It is interesting to note, that Hofmann-Engl's virtual pitch model computes for the octave 1 Schouten, the fifth 0.75 Schouten, the fourth 0.679 Schouten, the major third 0.56 Schouten, the minor sixth 0.513 Schouten, the major sixth 0.511 Schouten and for the minor third 0.49 Schouten. The minor second on the other end of the spectrum drops down to 0.182 Schouten. These computations might be seen as supporting Descartes's approach.
1.8. Andreas Werckmeister (November 30, 1645 – October 26, 1706)
With Werckmeister, questions on how to tune instruments draws to a close even if the introduction of the cent calculation still lies away more than 100 years from here. Werckmeister proposes a number of different tunings called Wohltemperierte Stimmung (well-proportioned tuning) leading towards equal temperament as outlined in his Musicalische Temperatur (1691). Particularly, the tuning with the fifths D - A, F# - C#, C# - G# and F - C narrowed down by a ¼ (Pythagorean) comma and the fifth G# - D# widened by the same amount we obtain a tuning which deviates from equal temperament by a mean of 2.6 cent only. Starting on C with 0 cent, we obtain the interval series:
0 96 204 300 396 504 600 702 792 900 1002 1098 [cent]
1.9. Leonhard Euler (15 April 1707 – 18 September 1783)
Euler produced, as a 24 years old mathematician, in 1731 the Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae (Attempt for a new music theory based on depicting in all clarity the evident principles of harmony). Not dissimilar to his predecessors, Euler relates the consonant/dissonant attribute of harmonies to ratios, but this time in relation to prime number factors. However, perhaps of more relevance for the future are his thoughts as expressed in Conjecture sur la raison de quelques dissonances généralement reçues dans la musique (Conjecture about the reason of some dissonances received in music) in 1764. Here, apparently for the first time in history, Euler suggests that the ear will tolerate small deviations from the exact ratios. This idea was finally confirmed in the 20th century through the discovery of categorical pitch perception pioneered by Houtsma in 1968.
1.10. Gustav Fechner (19 April 1801 – 28 November 1887)
Fechner as such was not a mathematician nor a music theorist, but an
experimental psychologist. However, his discovery of the Fechner
law is a fundamental prerequisite for both the cent and the sone calculation.
The Fechner law (sometimes also referred to as the Weber-Fechner law)
states that the intensity of a sensation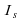
is proportional to the logarithm of the physical intensity
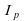of the stimulus. The law can be written as:
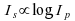or as
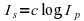with c as a constant
It is interesting to note that Ptolemy's understanding that ratio multiplication correlates to the addition of intervals implies, as shown by Hofmann-Engl (1989), the Fechner law.
1.11. Alexander John Ellis (14 June 1814 – 28 October 1890)
In 1885, Ellis published his paper called On the Musical Scales of various Nations in the Journal of the Society of Arts. Being aware that, in order to compare various scales and tuning system against each other, a robust measurement is needed, he introduced the cent calculation. The logarithmic definition is:
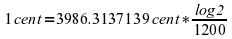
At times, the definition is given in the from that 1 cent is
the 1200 th part of an octave written as:
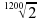
1.12. Hermann Ludwig Ferdinand von Helmholtz (31 August 1821 – 8 September 1894)
Helmhotltz's general importance as his specific importance within music might have been exaggerated by historians (not essentially different to the exaggeration of Albert Einstein's importance). In terms of music theory, Helmholtz wrote: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik (translated by Ellis in 1875 as On the Sensations of Tones and more literally: The teachings of sound sensations as the basis of music theory) which was published in 1863. Here, Helmholtz attaches dashes as pre- and suffixes to the musical letters (capital ones for the lower and lower case ones for the upper octaves) in order to differentiate between octaves.
1.13. Carl Stumpf (21 April 1848 – 25 December 1936)
Carl Stumpf wrote the book called Tonpsychologie (Sound/Musicpsychology). Perhaps most remarkable is his study on Consonance/Dissonance. Unlike his predecessors who had attempted to explain this phenomenon via ratios and prime number factors, Stumpf refers to the Verschmelzungsgrad (fusion degree) of intervals. This is, Stumpf asked participants within two experiments to relate to him whether they perceived simultaneously played intervals on an organ as one. The results of two experiments are recorded as:
|
Interval |
Fusion Degree (experiment 1) |
Fusion Degree (experiment 2) |
Octave |
76% |
- |
Fifth |
62% |
50% |
Fourth |
36% |
36% |
Major Third |
30% |
27% |
Minor Third |
- |
30% |
Minor Sixth |
19% |
- |
Triton |
15% |
24% |
It appears that for the first time ion history, a music theorist uses statistical tools measuring human responses in order to answer a question of music perceptual nature.
1.14. Stanley Smith Stevens (4 November 1906 – 18 January 1973)
If Ellis applied the Fechner Law to pitch perception, this time Stevens applies the same law to the perception of loudness in 1936 coining the term sone. However, Stevens exceeds the Fechner law as he computes sone by measuring the actual sound pressure and subtracting from it the perceptual threshold. The computation can be written as:
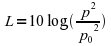or as
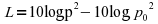
where L is the perceived loudness in sone, p the actual sound pressure measured in dB and po the perceptual threshold also measured in dB
1.15. J. F. Schouten (around 1940)
At the time of writing, no biographical details about J. F. Schouten have been available to the author. However, Schouten's paper The residue and the mechanism of hearing in: Proc. Kon. Akad. Wetenshap. 43 has been quoted in the literature frequently. Here, Schouten demonstrates that even by omitting some lower partials of the overtone series the pitch sensation of the first partial will be evoked. This is, overlaying the sine tones at the consecutive intervals of a fourth – major third – minor third – small minor third – large major second – major second – small major second produces the pitch sensation of a compound fifth below the first sine tone.
1.16. Wilhelm Fucks (4 June 1902 – 1 April 1990)
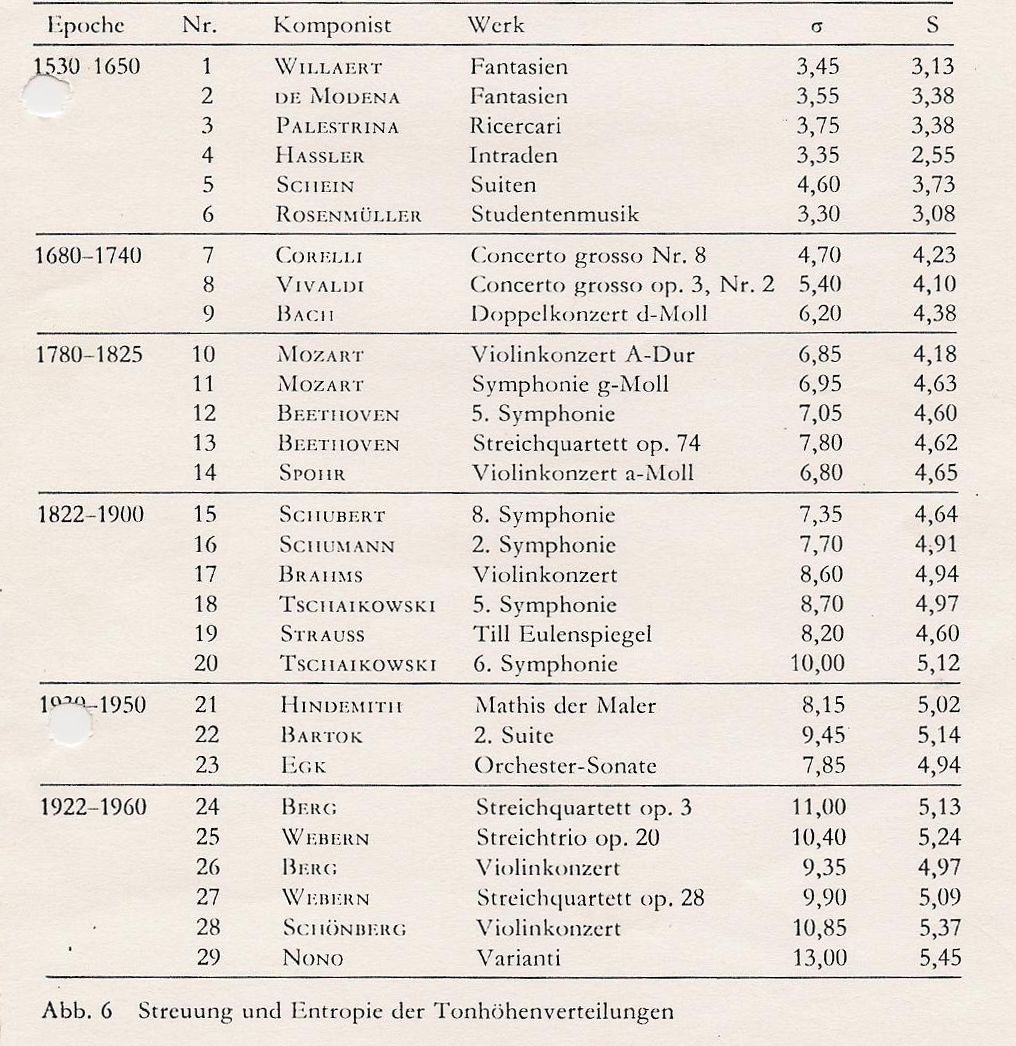
Wihelm Fucks published with co-author Joesef Lauter the Exatwissenschaftliche Musikanalyse (exact scientific music analysis) in 1965. The book appears never to have been translated into English and the German original is no longer available. It is not within the scope of this article to do justice to the whole book, but in order to give an insight into this work, the method and results of the first chapter will be presented here.
The team counted the occurrences of exact pitches within the works of 29
composers ranging from Willaert to Nono. Based on these counts they
computed the probability of occurrence i of each pitch within
each of the 29 pieces according to the formula:
.
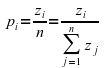They further computed sigma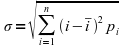
with
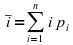and the entropy
.
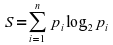Below are the results:
|
|
|
What this team attempted to demonstrate with this analysis is to show that over a period of nearly 500 years musical compositions had gained complexity measured as an increase in sigma and entropy values. Within the following chapters they continue to apply similar measures to various other parameters producing similar results.
1.17. Guerino Mazzola (born 1947)
Mazzola proposed a method of melodic transformations in 1990. For this purpose he made use of four transformation matrices. These matrices are:
Inversion as:
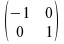
Retrograde as:
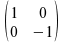
Parameter change as:
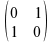
Arpeggio as:
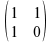
He then defines a melody as a vector consisting of a pitch component x and
a time component y as: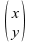
. Now, transforming this vector with the retrograde matrix, we obtain:
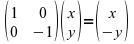
This is, the time line is now reversed. However as pointed out by
Hofmann-Engl (2003), inversion is not a reversal in time, but
reversing the order of the pitch sequence. Similar issues are pointed
out by Hofmann-Engl (2003) with the three remaining matrices and
particularly with the parameter change which is:
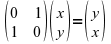, which
means that Mazzola now treats the time/duration and the
frequency/pitch dimension as interchangeable which is absurd from a
physical as well as from a cognitive point of view. However, it must
be noted that it appears that it was Mazzola who, for the first time in history,
used matrices in the context of melodic transformations.
1.18. Ludger Hofmann-Engl (born 1964)
Hofmann-Engl applies mathematical tools in three areas. These are 1) statistical music analysis, 2) virtual pitch and 3) melodic similarity.
1.18.1. Statistical music analysis
Clearly inspired by the work of Fucks, Hofmann-Engl applies statistical tools
to the analysis of a specific piece: The Passacaglia ungherese
by Ligeti 1988. Similar to our approach taken in the context of
Fucks, we will focus on one exemplary aspect only. Hofmann-Engl
firstly counts the occurrence of all pitches classified in pitch
classes for which he gives the formula:
.
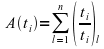He then computes the percentage of each pitch class occurring using the formula:
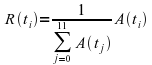. In case we have an equal distribution of pitch classes we would expect:
. He further defines the turbulence as:
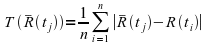and the significant deviation of occurrence as:
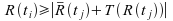. Applied to Ligeti's Passacaglia ungherese, he concludes that the pitch classes
d, e, g, a occur significantly more often, c and b occur regularly, c#, f and f# are non-significantly underrepresented and d#, g# and a# are significantly
underrepresented. After some further computation he arrives at the
following graph:
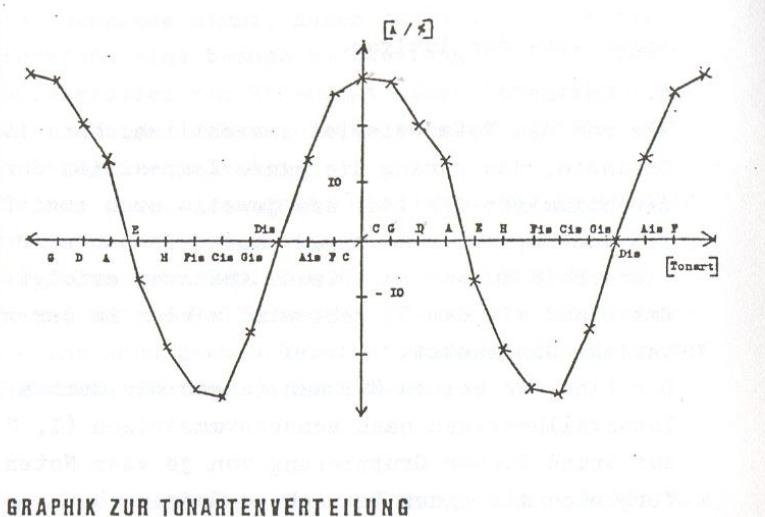
Here, the graph shows that c-major/a-minor are the key(s) which underpin the composition. Supported by a further harmonic analysis, Hofmann-Engl concludes that this composition is in a-minor leading to the summary conclusion that Ligeti made use of more contemporary harmonies in order to disguise the fact that the piece is actually in a traditional key.
1.18.2. Virtual Pitch
Hofmann-Engl further developed Terhardt's ideas in respect of virtual pitch during his postgraduate studies and presented within his unpublished MA thesis (1991). Additionally, he applied the model in various contexts, such as contemporary composition, music analysis, copy right infringement and Riemann's chord classification system, as presented during three international conferences (1999, 2006 & 2008) as well as in two papers published online (2004 & 2008). Recently, his model has been critically reviewed by Goldbach (2009). At the time of writing this model appears to be the most accurate virtual pitch model. The model is given as:
where V(t) is the strength of the virtual tone t, ws(si) the spectral weight of the ith subharmonic of the chord, wp(si) the weight of the ith subharmonic according to the position of the tone within the chord, n the number of tones the chord consists of and the constant c = 6 Hh
A second part of the model calculates the consonance/dissonance degree, called the sonance to any given chord and is given as:
where S(ch) is the sonance (with unit Sh = Schouten) of the chord ch, vmax is the virtuality of the strongest root, k = 6 Hh/Sh, m is the number of virtual pitches produced by the chord ch, vpmax is the virtuality of the strongest root in percent (= vmax divided by the sum of all virtual pitches of the chord ch), c = 0.223 (the maximal limit the strongest root can fetch), n the number of tones the chord ch consists of and i the ith tone of the chord ch.
1.183. Melodic similarity
Here, Hofmann-Engl (PhD thesis 2003 and published 2009) represents melodies as composed of melota (pitch sequences), dynama (dynamic sequences) and chronota (durational sequences). These parameters are then represented as n+1 dimensional vectors. This is:
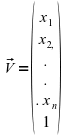
This vectors are then transformed via transformation matrices of the following two types:
Translation
matrix as:
Reflection
matrix as:
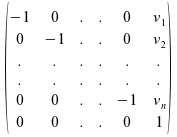
A thank you to Yan-Tak Lau-Davies for providing the information on Jing Fang and Sima Biao.
